Arbori
Arborii sunt
structuri de date dinamice şi omogene. Cele mai comune utilizări ale
arborilor sunt căutarea în volume mari de date şi reprezentarea de
structuri organizate ierarhic.
1. Arbori oarecare
Arborii oarecare
sunt colecţii de noduri care conţin informaţia utilă
şi legături către descendenţi. Fiecare arbore conţine
un nod iniţial numit rădăcină.
Structura unui arbore oarecare este
prezentată în figura următoare:
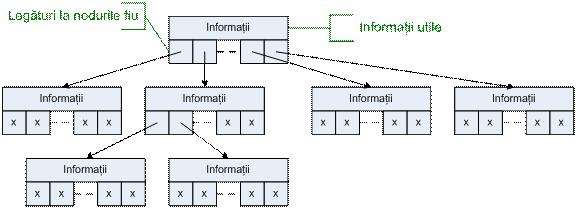
Pentru implementarea unui arbore oarecare în C/C++ se poate folosi o
structură de forma:
// tipul de date al informatiilor utile
typedef double TipArbore;
// structura care reprezinta un nod din arbore
struct NodArbore
{
// informatiile utile stocate in nod
TipArbore
Informatii;
// numarul de legaturi catre fii
int numarLegaturi;
// vector de legaturi catre fii
NodArbore
**Legaturi;
};
Fiecare nod
conţine informaţiile utile, un întreg care reţine numărul
de fii şi un vector de pointeri către fii.
Principalele operaţii care pot fi implementate pe un arbore oarecare sunt:
|
Operaţie |
Descriere |
|
Adăugare nod |
Adaugă un nod în arbore după un anumit criteriu (de exemplu la
un anumit nod părinte). Operaţia presupune alocarea memoriei pentru
nod, copierea informaţiei utile şi modificarea legăturii
părintelui. |
|
Ştergere nod |
Presupune dealocarea memoriei pentru nodul respectiv şi pentru
toţi descendenţii săi şi modificarea legăturii
părintelui. |
|
Parcurgere arbore |
Presupune obţinerea unei liste care conţine toate
informaţiile utile din arbore. |
|
Căutare element |
Presupune obţinerea unui pointer la un nod pe baza unui criteriu de
regăsire. |
Exemplu de operaţie – ştergerea unui nod:
// sterge un nod
din arbore primind ca parametru
// o referinta la
legatura parintelui
void
StergereNod(NodArbore* &legaturaParinte)
{
// stergem nodul si subarborele
corespunzator
StergereSubarbore(legaturaParinte);
// modificam legatura paeintelui
legaturaParinte = NULL;
}
// sterge
recursiv un subarbore
void
StergereSubarbore(NodArbore *nod)
{
// conditia de oprire din recursie
if (nod == NULL)
return;
// stergem subarborii
for (int
i = 0; i < nod->numarLegaturi; i++)
StergereSubarbore(nod->Legaturi[i]);
// stergem nodul curent
delete [] nod->Legaturi; // stergem vectorul
de legaturi
delete [] nod; // stergrm nodul
}
2. Arbori binari
Arborii binari sunt arbori în care nodurile conţin cel mult doi descendenţi. Pentru memorarea acestor arbori se poate folosi o structură mai simplă de forma:
// tipul de date
al informatiilor utile
typedef double TipArbore;
// structura care
reprezinta un nod
// dintr-un
arbore binar
struct NodArbore
{
// informatiile utile stocate in nod
TipArbore Informatii;
// vector de legaturi catre fii
NodArbore *Stanga, *Dreapta;
};
Operaţiile sunt
aceleaşi ca şi în cazul arborilor oarecare.
Exemplu: parcurgerea arborelui în ordinea stânga – rădăcină - dreapta şi stocarea elementelor într-o listă:
// nodul listei simplu inlantuite
struct NodLista
{
// informatia utila
TipArbore
Informatii;
// legastura catre elementul urmator
NodLista
*Legatura;
// constructorul pentru initializarea unui nod
NodLista(TipArbore
info, NodLista* leg = NULL)
:
Informatii(info), Legatura(leg) {}
};
// functie de concatenare a doua liste simplu inlantuite
NodLista* Concatenare(NodLista *cap1, NodLista *cap2)
{
// cazul 1: prima lista e vida
if (cap1 == NULL)
return cap2;
// cazul 2: prima lista e nevida
// parcurgem prima lista
while (cap1->Legatura != NULL)
cap1 =
cap1->Legatura;
// si facem legatura
cap1->Legatura
= cap2;
// intoarcem capul listei
return cap1;
}
// procedura recursiva de parcurgere a unui arbore binar
NodLista* Parcurgere(NodArbore *nod)
{
// conditia de oprire din recursie
if (nod == NULL)
return NULL;
// initializam lista
NodLista *cap =
NULL;
// adaugam subarborele stang
cap =
Concatenare(cap, Parcurgere(nod->Stanga));
// adaugam nodul curent
cap =
Concatenare(cap, new
NodLista(nod->Informatii));
// adaugam subarborele drept
cap =
Concatenare(cap, Parcurgere(nod->Dreapta));
return cap;
}
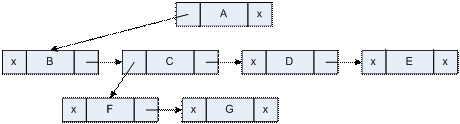
Arborii oarecare pot fi memoraţi ca arbori binari schimbând semantica legăturilor nodului astfel:
·
legătura
stânga va adresa primul fiu
·
legătura
dreapta va adresa următorul frate
Exemplu de
transformare:
a) arbore
oarecare:
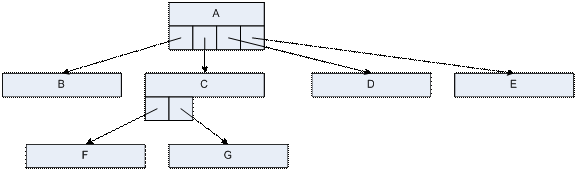
b) arbore
oarecare memorat ca arbore binar:
3. Arbori binari de căutare
Arborii binari de
căutare sunt arbori binari în care nodurile sunt memorate ordonat în
funcţie de o cheie. Toate nodurile din arbore au în subarborele stâng noduri
care au chei mai mici şi în subarborele drept chei mai mari.
Arborii de
căutare permit regăsirea rapidă a informaţiilor (O(log2 n)) atât timp cât arborele este echilibrat. În cazul cel mai defavorabil,
timpul de căutare este identic cu cel al unei liste simplu
înlănţuite.
Operaţiile de bază pe un arbore de căutare sunt următoarele:
|
Operaţia |
Algoritmul |
|
Căutare |
Se compara cheia cu nodul curent. Dacă este mai egală, am
găsit nodul, dacă este mai mică căutăm în
subarborele stâng, altfel căutăm în subarborele drept.
Căutarea se opreşte când nodul a fost găsit sau s-a atins baza
arborelui. |
|
Adăugare |
Se caută folosind algoritmul de căutare poziţia în arbore
şi se alocă memoria şi se face legătura cu nodul
părinte. |
|
Ştergere |
Se caută nodul de şters şi se şterge nodul.
Subarborele drept este avansat în locul nodului şters, iar subarborele
stâng este mutat ca fiu al celui mai mic element din subarborele drept. |
Implementarea operaţiilor de bază este prezentată în următoarea bibliotecă:
#ifndef ARBORE_H
#define ARBORE_H
// un nod din arbore
struct NodArbore
{
// informatia utila
TipArbore Date;
// legaturile catre subarbori
NodArbore
*Stanga, *Dreapta;
// constructor pentru initializarea unui nod nou
NodArbore(TipArbore
date,
NodArbore
*stanga = NULL, NodArbore *dreapta = NULL) :
Date(date),
Stanga(stanga), Dreapta(dreapta){}
};
// Arborele este manipulat sub
// forma unui pointer catre radacina
typedef NodArbore*
Arbore;
// Creaza un arbore vid
Arbore ArbCreare()
{
return NULL;
}
// Testeaza daca un arbore este vid
bool
ArbEGol(Arbore& arbore)
{
return arbore == NULL;
}
// Adauga un element intr-un arbore de cautare
void
ArbAdauga(Arbore& arbore, TipArbore date)
{
// Cazul 1: arbore vid
if (ArbEGol(arbore))
{
arbore = new NodArbore(date);
return;
}
// Cazul 2: arbore nevid
if (date < arbore->Date)
// daca exista subarborele stang
if (arbore->Stanga != NULL)
// inseram in subarbore
ArbAdauga(arbore->Stanga,
date);
else
// cream subarborele stang
arbore->Stanga
= new NodArbore(date);
if (date > arbore->Date)
// daca exista subarborele drept
if (arbore->Dreapta != NULL)
// inseram in subarbore
ArbAdauga(arbore->Dreapta,
date);
else
// cream subarborele drept
arbore->Dreapta
= new NodArbore(date);
}
// Functie privata de stergere a unui nod
void
__ArbStergeNod(Arbore& legParinte)
{
// salvam un pointer la nodul de sters
Arbore nod =
legParinte;
// daca avem un subarbore drept
if (nod->Dreapta != NULL)
{
// facem legatura
legParinte
= nod->Dreapta;
// daca avem si un subarbore stang
if (nod->Stanga)
{
// cautam cel mai mic element din subarborele drept
Arbore
temp = nod->Dreapta;
while (temp->Stanga != NULL)
temp
= temp->Stanga;
// si adaugam subarborele stang
temp->Stanga
= nod->Stanga;
}
}
else
// daca avem doar un subarbore stang
if (nod->Stanga != NULL)
// facem legatura la acesta
legParinte
= nod->Stanga;
else
// daca nu avem nici un subnod
legParinte
= NULL;
// stergem nodul
delete nod;
}
// Sterge un nod dintr-un arbore de cautare
void
ArbSterge(Arbore& arbore, TipArbore date)
{
// Cazul 1: arbore vid
if (ArbEGol(arbore))
return;
// Cazul 2: stergere radacina
if (arbore->Date == date)
{
// salvam un pointer la radacina
Arbore nod
= arbore;
// daca avem un subarbore drept
if (nod->Dreapta)
{
// facem legatura
arbore
= nod->Dreapta;
// daca avem si un subarbore stang
if (nod->Stanga)
{
// cautam cel mai mic element din subarborele drept
Arbore
temp = nod->Dreapta;
while (temp->Stanga != NULL)
temp
= temp->Stanga;
// si adaugam subarborele stang
temp->Stanga
= nod->Stanga;
}
}
else
// daca avem doar un subarbore stang
if (nod->Stanga != NULL)
// facem legatura la acesta
arbore
= nod->Stanga;
else
// daca nu avem nici un subnod
arbore
= NULL;
// stergem vechea radacina
delete nod;
return;
}
// Cazul 3: stergere nod in arbore nevid
// cautam legatura la nod in arbore
// si stergem nodul (daca exista)
Arbore nodCurent
= arbore;
while (true)
{
if (date < nodCurent->Date)
if (nodCurent->Stanga == NULL)
break; // nodul nu exista
else
if (nodCurent->Stanga->Date == date)
// nodul de sters este descendentul stang
__ArbStergeNod(nodCurent->Stanga);
else
// continuam cautarea in subarborele stang
nodCurent = nodCurent->Stanga;
else
if (nodCurent->Dreapta == NULL)
break; // nodul nu exista
else
if (nodCurent->Dreapta->Date == date)
// nodul de sters este descendentul drept
__ArbStergeNod(nodCurent->Dreapta);
else
// continuam cautarea in subarborele stang
nodCurent = nodCurent->Dreapta;
}
}
// Cauta recursiv un nod in arborele de cautare
bool
Cautare(Arbore& arbore, TipArbore info)
{
// conditia de oprire din recursie
if (arbore == NULL)
return false;
// verificam daca am gasit nodul
if (arbore->Date == info)
return true;
// daca cheia este mai mica
if (arbore->Date < info)
// cautam in subarborele stang
return Cautare(arbore->Stanga, info);
else
// altfel cautam in subarborele drept
return Cautare(arbore->Dreapta, info);
}
#endif //ARBORE_H
Parcurgerea
unui arbore de căutare în ordinea stânga – rădăcină –
dreapta conduce la obţinerea listei nodurilor în ordinea crescătoare
a cheilor. Funcţia următoare afişează în ordine elementele
unui arbore binar de căutare:
void
AfisareSRD(Arbore& arbore)
{
if (ArbEGol(arbore))
return;
AfisareSRD(arbore->Stanga);
cout << arbore->Date << " ";
AfisareSRD(arbore->Dreapta);
}
Parcurgerea nerecursivă a unui arbore binar de căutare se poate face folosind o stivă:
void
TraversareNerecursiv(Arbore& arbore)
{
Stiva stiva = StCreare();
// a) ne deplasam pana la primul nod
Arbore nod = arbore;
while (nod != NULL)
{
StAdauga(stiva, nod);
nod = nod->Stanga;
}
if (!StEGoala(stiva))
cout << StVarf(stiva)->Date << "
";
// b) traversam arborele in inordine
Arbore parinte, copil;
while (!StEGoala(stiva))
{
parinte = StExtrage(stiva);
copil = parinte->Dreapta;
while (copil != NULL)
{
StAdauga(stiva, copil);
copil = copil->Stanga;
}
if (!StEGoala(stiva))
cout << StVarf(stiva)->Date <<
" ";
}
}
4. Alte tipuri de arbori
Arbori AVL
Arborii AVL
(Adelson-Veliskii şi Landis) elimină neajunsul major al arborilor
binari: faptul că viteza
de căutare depinde de ordinea în care sunt introduse cheile în arbore.
Arborii AVL permit obţinerea unei viteze de căutare constante de
complexitate O(n log2n)
prin garantarea faptului că arborele este echilibrat la orice moment.
Structura unui
nod este cea a unui nod de arbore binar la care se mai adaugă un câmp numit
BF (Balance Factor) care
reprezintă diferenţa dintre înălţimea subarborelui drept
(RH) şi înălţimea subarborelui stâng (LH). Fiecare nod dintr-un
AVL are proprietatea că înălţimea subarborelui stâng diferă
de înălţimea subarborelui drept cu cel mult o unitate, deci BF va avea
una din valorile -1, 0 sau 1.
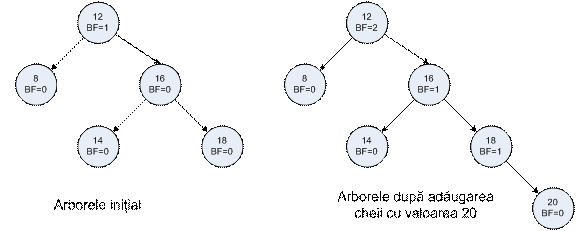
Adăugarea şi ştergerea nodurilor se face la fel ca în cazul arborilor binari de căutare. După adăugarea/ştergerea unui nod, se recalculează BF-ul pentru nodurile arborelui. Exemplu:
Dacă în urma
unei operaţii de adăugare sau ştergere arborele nu mai este
echilibrat (BF Ď {-1,0,1}), acesta trebuie echilibrat. Echilibrarea în cazul arborilor AVL se face
prin intermediul operaţiei de rotire la stânga (BF>1) sau la dreapta (BF<1). Pivotul în jurul căruia se face
rotirea este cel mai de jos nod care are BF Ď {-1,0,1}. Procedeul de rotire continuă până în
momentul în care arborele redevine echilibrat.
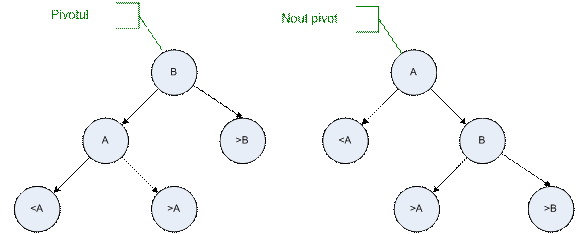
Rotirea se face după modelul următor:
1.
rotire
la dreapta
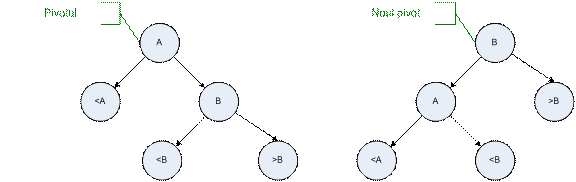
2.
rotire
la stânga
Căutarea în arborii AVL se face la fel ca în
arborii binari de căutare.
Arbori B
Arborii B (de la
Balanced) sunt arbori de căutare echilibraţi
proiectaţi pentru lucrul cu volume
foarte mari de date (stocate pe suporturi de memorie externă).
Proprietăţile definitorii ale arborilor B sunt:
1. Toate nodurile au următoarele câmpuri:
a.
n – numărul de chei stocate în nod
b. k1,…,kn – cheile stocate în nod cu proprietatea k1<k2<…<kn
c. c1,…,cn+1 – pointeri la subarbori
2.
Toate
cheile din subarborele indicat de ci
sunt cuprinse între ki-1<ki;
cheile din subarborele indicat de c1
sunt mai mici decât k1,
iar cele din subarborele indicat de cn+1
sunt mai mari decât kn
3.
Toate
nodurile frunză se află la acelaşi nivel h
4.
Fiecare
arbore B are asociat un grad t>2. Toate nodurile, cu excepţia rădăcinii
trebuie să aibă între t-1
şi 2t-1 noduri
Cele două avantaje majore ale arborilor B care îi recomandă pentru folosirea în situaţiile în care este necesară prelucrarea unui volum mare de date sunt:
·
permite
citirea mai multor chei la un singur acces la disc (gradul t este ales astfel
încât dimensiunea unui nod corespunde dimensiunii unei pagini de disc)
·
necesită
accesarea a foarte puţine pagini pentru a efectua o căutare (![]() )
)
Principalele operaţii care se efectuează
pe un astfel de arbore sunt căutarea, adăugarea de chei şi
ştergerea de chei.
Căutarea se face similar cu căutarea într-un arbore binar după următorul algoritm:
|
i = 1 |
|
|
while i <= nod.n and cheie > nod.k[i] |
// căutam
cheia în nodul curent |
|
i = i + 1 |
|
|
if i <= nod.n and cheie = nod.k[i] |
//
verificăm dacă am găsit nodul |
|
return (nod, i) |
|
|
if nod.c[i] != nul |
// dacă nu
este nod frunză |
|
return cautare(nod.c[i],
cheie) |
//
continuăm căutarea |
|
else |
// altfel
înseamnă că avem un nod |
|
return nul |
// frunză
şi oprim căutarea |
Adăugarea unei chei se face recursiv printr-o singură parcurgere în următorii paşi:
1.
Dacă
nodul rădăcină este plin (are 2t-1 chei), atunci se descompune.
2.
Se
porneşte procedura recursivă care parcurge arborele ca la
căutare şi execută următoarele acţiuni pentru fiecare
nod:
a.
Dacă
nodul este nod frunză se inserează cheia.
b.
Dace
nu este nod frunză:
i.
Dacă
nodul copil este plin se descompune.
ii.
Se
apelează procedura pentru nodul copil.
Operaţia de descompunere a unui nod cu 2t-1 chei presupune găsirea elementului median al nodului, mutarea acestuia în nodul părinte sau crearea unui nod nou în cazul rădăcinii şi descompunerea nodului iniţial în două noduri cu t-1 chei. Exemplu de descompunere:
|
|
|
|
a) nodul iniţial |
b) nodul descompus |
Se observă
că toate inserările se fac într-un nod frunză, iar arborele
creşte în sus, de la rădăcină, prin intermediul
operaţiei de descompunere.
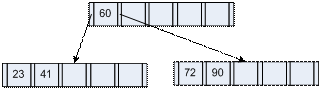
Pentru exemplificare vom considera următorul arbore B de grad t=2 (fiecare nod cu excepţia rădăcinii va avea între 2 şi 5 chei) cu două nivele:
|
|
|
a) arborele iniţial |
|
|
|
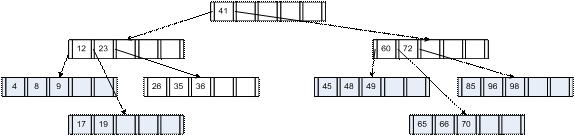
b) arborele după inserarea
elementului 19 |
|
|
|
c) arborele după inserarea elementului 12 (descompunere nod intern) |
|
|
|
d) arborele după inserarea elementului 36 (descompunere nod rădăcină) |
Ştergerea unei chei se face similar cu adăugarea. Păstrarea proprietăţilor arborelui B în urma ştergerii unei chei se face prin două mecanisme:
·
coborârea
unei chei din nodul părinte/fiu în cazul în care acesta are cel puţin
t chei sau este nodul
rădăcină
·
recompunerea
nodului rădăcină în situaţia în care nodul
rădăcină are 1 cheie şi nodurile copil au câte t-1 chei (astfel se realizează
scăderea înălţimii arborelui)
5. Probleme
1.
Scrieţi
funcţia pentru numărarea elementelor dintr-un arbore oarecare.
2.
Scrieţi
funcţia pentru transformarea unui arbore oarecare într-o listă simplu
înlănţuită prin parcurgerea acestuia.
3.
Scrieţi
funcţiile pentru determinarea elementului minim şi elementului maxim
dintr-un arbore binar de căutare.
4.
Scrieţi
funcţia pentru afişarea în ordine a elementelor dintr-un arbore binar
de căutare.
5.
Scrieţi
o funcţie iterativă pentru căutarea unui element într-un arbore
de căutare.
6.
Scrieţi
funcţia de concatenare a doi arbori binari de căutare (funcţia
de adăugare în arbore se presupune creată în prealabil).
7.
Scrieţi
funcţia pentru determinarea celui mai apropiat părinte comun a
două noduri dintr-un arbore binar.
8.
Precizaţi
cum va arăta un arbore AVL după introducerea cheilor 12, 8, 5, 77,
12, 88, 92, 93, 94, 95, 7, 8, 9.
9.
Precizaţi
cum va arăta un arbore B de grad 3 după introducerea cheilor 12, 8,
5, 77, 12, 88, 92, 93, 94, 95, 7, 8, 9.
10.
O
societate de investiţii deţine o bază de aproximativ 8 000 000 clienţi. Precizaţi ce structură de date
trebuie folosită pentru a permite o regăsire rapidă a
clienţilor pe baza codului numeric personal şi argumentaţi
alegerea.