Masive de date
Masivele sunt structuri de
date omogene cu un numar finit si cunoscut de elemente, ce ocupa un spatiu
contiguu de memorie.
Un masiv este caracterizat de
urmatoarele elemente:
- numele
- tipul de data asociat
- numarul de dimensiuni
- numarul de elemente pentru fiecare dimensiune
1. Vectori
Descriere generala
Vectorii sunt masive
unidimensionale. In C++ vectorii se declara folosind sintaxa:
tip
nume[n]
unde:
- tip – tipul de data folosit; poate fi unul din
tipurile de baza (int, float, char, …) sau un tip definit de utilizator (articole, obiecte)
- nume – numele prin care va fi referit vectorul
- n – numarul de elemente eale vectorului
Exemple de declaratii:
// vector de 100 valori intregi
int vanzari[100];
// vector de 15 valori reale
float temperaturi[15];
Memorarea vectorilor se face
intr-un spatiu continuu de memorie. Numele vectorului este de fapt un pointer
catre adresa primului element. Pentru o declaratie de forma int v[5]; reprezentarea
in memoria interna este:
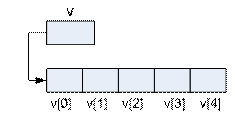
Dimensiunea totala a vectorului
este calculata ca produs intre numarul de elemente si dimensiunea unui element.
Initializarea vectorului se
poate face la declarare printr-o constructie de forma:
tip
nume[]={lista_valori}
Se observa ca in acest caz nu
este necesara precizarea numarului de elemente. Acesta va fi dedul automat de
compilator din dimensiunea listei cu care se face initializarea. In cazul in
care numarul de elemente precizat este mai mare decat numarul de elemente din
lista se va realiza o initializare partiala a vectorului.
Exemple de initializari la
declarare:
// initializare fara precizarea
explicita
// a numarului maxim de elemente
int v1[] = {1, 2, 3, 4, 5};
// initializare completa cu
precizarea
// numarului maxim de elemente
int v2[3] = {17, 19, 23};
// initializare partiala
int v3[5]
= {7, 6, 5};
Accesul la elementele vectorului
se face direct; compilatorul calculeaza adresa elementului pe baza indexului si
a dimensiunii unui element. Numerotarea elementelor se face incapand cu zero.
Pentru un vector v cu n elemente referirea elementelor se face
folosind v[0], v[1], v[2], …, v[n-1].
Exemple:
// citeste al treilea element din
vector
int a = v1[2];
// modifica valoarea celui de-al
doilea element
v1[1] = 7;
Vectorii pot fi trimisi ca
parametrii in functii direct prin nume urmat de paranteze drepte. Toate
modificarile efectuate de catre functie asupra valorilor stocate in vector vor
fi vizibile si in apelator Acest lucru este posibil datorita faptului ca prin
nume se transfera de fapt adresa primului element din vector.
Operatii de baza
Citire de la tastatura:
int CitireVector(int vector[], int
nrMaxElemente)
{
// Citirea numarului efectiv de
elemente
// cu validare
int nrElemente;
do
{
cout << "Numar elemente:";
cin >> nrElemente;
}
while(nrElemente < 0 ||
nrElemente > nrMaxElemente);
// Citirea elementelor vectorului
for (int
i = 0; i < nrElemente; i++)
{
cout << "Elementul " << i
<< ":";
cin >> vector[i];
}
// intoarcem numarul efectiv de elemente
return nrElemente;
}
Afisare pe monitor:
void AfisareVector(int vector[], int
nrElemente)
{
// parcurgerea si afisarea
vectorului
for (int
i = 0; i < nrElemente; i++)
cout << vector[i] << " ";
cout << endl;
}
Cautare element dupa valoare:
int CautareElementVector(int vector[], int
nrElemente, int valoare)
{
// parcurgem vectorul
for (int
i = 0; i < nrElemente; i++)
if (vector[i] ==
valoare)
return i;
// element negasit
return -1;
}
Inserare element:
void InserareElement(int vector[], int
nrElemente, int pozitia, int valoare)
{
// se presupune ca dimensiunea
maxima a vectorului
// este cel putin egala cu
nrElemente + 1
if (pozitia == nrElemente)
// inserare la sfarsitul
vectorului
vector[nrElemente] = valoare;
else
{
// inserare in interiorul
vectorului
// trebuie sa deplasam la
dreapta elementele
// aflate dupa pozitia de
inserare
for (int i = nrElemente; i > pozitia; i--)
vector[i] = vector[i-1];
// si inseram elementul
vector[pozitia] = valoare;
}
}
Stergere element:
void StergereElement(int vector[], int
nrElemente, int pozitia)
{
// trebuie sa deplasam la stanga
elementele
// aflate dupa pozitia de stergere
for (int
i = pozitia; i < nrElemente; i++)
vector[i] = vector[i+1];
}
Sortare vector:
void SortareVector(int vector[], int
nrElemente)
{
// sortare prin selectie
for (int
i = 0; i < nrElemente-1; i++)
{
// cautam minimul in
elementele ramase
int minim = vector[i];
int pozitie = i;
for (int j = i + 1; j < nrElemente; j++)
if (minim >
vector[j])
{
minim = vector[j];
pozitie = j;
}
// interschimbam elementul
minim cu elementul curent
vector[pozitie] = vector[i];
vector[i] = minim;
}
}
2. Matrice
Descriere generala
Matricele sunt masive
unidimensionale. Sintaxa de declarare este:
tip
nume[m][n]
unde:
- tip – tipul de data folosit; poate fi unul din
tipurile de baza (int, float, char, …) sau un tip definit de utilizator (articole, obiecte)
- nume – numele prin care va fi referita matricea
- m – numarul de linii din matrice
- n – numarul de coloane din matrice
Exemple de declaratii:
// matrice de intregi cu 10 linii si
10 coloane
int vanzari[10][10];
// vector de valori reale
float temperature[3][15];
Memorarea matricelor se face,
ca si in cazul vectorilor, intr-un spatiu continuu de memorie. Numele matricei un
pointer catre adresa primului element. Elementele matricei dunt stocate in
memorie linie dupa linie.
Pentru o declaratie de forma float m[2][3] reprezentarea
in memoria interna este:
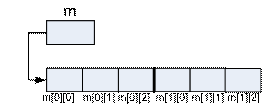
Dimensiunea totala a matricei
este calculata ca produs intre numarul de linii, numarul de coloane si
dimensiunea unui element.
Initializarea matricei se
poate face la declarare printr-o constructie de forma:
tip
nume[][n]={{lista_valori1}, {lista_valori2}, …, {lista_valorim}}
Se observa ca in acest caz nu
este necesara precizarea numarului de elemente asociat primei dimensiuni.
Acesta va fi dedus automat de compilator din dimensiunea listei cu care se face
initializarea. In cazul in care numarul de linii precizat este mai mare decat
numarul de elemente din listae se va realiza o initializare partiala a matricei.
Exemple de initializari la
declarare:
// initializare fara precizarea
explicita
// a numarului de linii
int m1[][2] = {{1, 2}, {3, 4}, {5,
6}};
// initializare completa cu
precizarea
// numarului de linii si coloane
int m2[2][3] = {{17, 19, 23},
{29, 31, 37}};
// initializare partiala
int m3[2][5]
= {{7, 6}, {5}};
Accesul la elementele matricei
se face direct; compilatorul calculeaza adresa elementului pe baza liniei, a
coloanei, a numarului de elemente pe linie si a dimensiunii unui element. Formula
folosita este:
adr(m[i][j]) = adr(m[0][0]) +
(i * nr_max_elemente_linie + j) * dim_element
Numerotarea liniilor si a
coloanelor se face incepand cu zero.
Exemple de accesare elemente:
// citeste al doilea element de
// pe a doua linie din matrice
int a = m2[1][1];
// modifica primul element
m2[0][0] = 7;
Transmiterea ca parametri se
face ca si in cazul vectorilor prin numele masivului. Problema care apare in
cazul matricelor este aceea ca numarul de coloane trebuie fixat pentru a
permite calcularea de catre compilator a adresei elementelor. In cazul in care
se doreste lucrul cu matrice oarecare, transmiterea se va face prin pointeri
iar adresa elementelor se va calcula dupa formula prezentata anterior. In acest
caz va trebui trimisa ca parametru atat dimensiunea maxima a matricei cat si
dimensiunea minima a acesteia.
Operatii de baza
Citire de la tastatura:
void CitireMatrice(int *matrice, int
nrMaxLinii, int nrMaxColoane, int& nrLinii, int&nrColoane)
{
// Citirea numarului efectiv de
elemente
// cu validare
do
{
cout << "Numar linii:";
cin >> nrLinii;
}
while(nrLinii < 0 ||
nrLinii > nrMaxLinii);
do
{
cout << "Numar coloane:";
cin >> nrColoane;
}
while(nrColoane < 0 ||
nrColoane > nrMaxColoane);
// citirea elementelor
for(int
i = 0; i < nrLinii; i++)
for(int j = 0; j < nrColoane; j++)
{
cout << "Elementul (" << i
<< "," << j << "):";
cin >> *(matrice + i*nrMaxLinii + j);
}
}
Citire de la tastatura:
void AfisareMatrice(int *matrice, int
nrMaxLinii, int nrMaxColoane, int nrLinii, int
nrColoane)
{
// afisarea elementelor
for(int
i = 0; i < nrLinii; i++)
{
// afisarea liniei
for(int j = 0; j < nrColoane; j++)
cout << *(matrice + i*nrMaxLinii + j)
<< " ";
// linie noua
cout << endl;
}
}
Cautare element dupa valoare:
void CautareElement(int *matrice, int
nrMaxLinii, int nrMaxColoane, int nrLinii, int
nrColoane, int valoare, int& x, int& y)
{
// element negasit
x = y = -1;
for(int
i = 0; i < nrLinii; i++)
for(int j = 0; j < nrColoane; j++)
if ( (*(matrice
+ i*nrMaxLinii + j)) == valoare)
{
// valoare
gasita
x = i;
y = j;
return;
}
}
3. Liniarizare matrice si matrice rare
In practica apar cazuri in care matricele au anumite caracteristici care permit o stocare mai eficienta decat cea standard. Exemple de asemenea matrice sunt: matricele diagonale, matricele simetrice si matricele rare.
Principalele tehnici folosite in astfel de cazuri sunt liniarizarea matricelor si stocarea sub forma de matrice rare.
Liniarizarea matricelor presupune stocarea elementelor semnificative ale matricei intr-un vector si construirea de functii specializate pentru simularea accesului direct la elemente.
Matricele diagonale sunt matrice patratice de dimensiune n care contin elemente nenule numai pe diagonala principala:
|
7 |
0 |
0 |
|
0 |
2 |
0 |
|
0 |
0 |
11 |
In acest caz memorarea se va face folosind un vector de dimensiune n care va memora elementele de pe diagonala principala. Accesul la elementul i, j se va face folosind functiile:
int CitireValoare(int* matrice, int n, int i, int j)
{
if (i != j)
// daca nu este element de pe
diagonala principala
return 0;
else
// element de pe diagonala
return matrice[i];
}
void ScriereValoare(int* matrice, int n, int i, int j, int valoare)
{
// scrierea se face doar daca este
// element de pe diagonala principala
if (i == j)
matrice[i] = valoare;
}
Exemplu de utilizare:
// declarare si initializare
int matDiag[3] = {7, 2, 11};
// citire valoare
int val1 =
CitireValoare(matDiag, 3, 1, 2);
// scriere valoare (1, 1);
ScriereValoare(matDiag, 3, 1, 1, 5);
Matricele simetrice sunt
matrice patratice in care corespondente de sub si de peste diagonala principala
sunt egale (adica m[i][j] = m[j][i] pentru oricare i si j). In acest caz se va
folosi un vector care va contine numai elementele de peste si de pe diagonala
principala.
Matricea
|
1 |
2 |
3 |
4 |
|
2 |
5 |
6 |
7 |
|
3 |
4 |
8 |
9 |
|
7 |
8 |
9 |
10 |
va fi liniarizata sub forma:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Calculul pozitiei elementului
i,j dintr-o matrice de dimensiune n se face dupa formula:
![]() pentru j <= i. Daca j > i, atunci se interschimba i cu j.
pentru j <= i. Daca j > i, atunci se interschimba i cu j.
Functia de acces la elemente este:
int& Valoare(int* matrice, int n, int i, int j)
{
// interschimbam elementele daca
este cazul
if (j > i)
{
int t = j;
j = i;
i = t;
}
// calculam pozitia
int pozitia = i*n + (i*(i-1))/2 + j;
return matrice[pozitia];
}
Exemplu de utilizare:
// declarare si initializare
int matSim[10] = {1, 2, 3, 4,
5, 6, 7, 8, 9, 10};
// citire valoare
int val1 = Valoare(matSim, 4,
1, 2);
// scriere valoare (1, 1);
Valoare(matSim, 4, 1, 1) = 7;
Aceeasi tehnica se poate aplica si in cazul matricelor
triunghiulare.
Matricele rare sunt matrice
care au majoritatea elementelor nule (mai mult doua treimi). In acest caz este
mai eficient sa memoram matricea sub forma a trei vactori care sa contina
linia, coloana si valoarea pentru elementele nenule.
Pentru matricea:
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
23 |
|
0 |
7 |
0 |
0 |
|
0 |
0 |
0 |
0 |
vom avea vectorii:
|
Linii: |
1 |
2 |
|
Coloane: |
3 |
1 |
|
Valori: |
23 |
7 |
Alternativ, putem stoca
elementele intr-un singur vector de articole care sa contina linia, coloana si
valoarea pentru fiecare element nenul.
4. Probleme
1. Se considera o multime formata din N activitati ale caror coduri sunt numere naturale ordonate crescator. Memorarea codurilor este realizata intr-un masiv unidimensional X avand N componente.
Sa se scrie procedurile care permit actualizarea listei de activitati prin:
inserarea codului unei noi activitati in asa fel incat sirul activitatilor sa ramana crescator
eliminarea unei activitati al carui cod este specificat.
2. Se considera un magazin si volumele vanzarilor pe trei luni, inregistrate separat zide zi.
Sa se concateneze cele trei siruri de date, pentru a obtine inregistrarile la nivelul unui trimestru.
3. Se considera un lant de 5 magazine si nivelurile valorice ale vanzarilor zilnice.
Conducerea doreste sa cunoasca:
valoarea zilnica a vanzarilor la nivelul intregului lant de magazine
valoarea lunara a vanzarilor fiecarui magazin
valoarea lunara a vanzarilor intregului lant de magazine
4. Se considera judetele si valoarea productiei de origine vegetala si de origine animala. Se pune problema stabilirii judetelor care acopera cel putin 90% din valoarea productiei agricole.
5. Sa se scrie programul care memoreaza intr-o structura de date adecvata elementele unei matrice triunghiulare, cu elementele nenule situate deasupra diagonalei principale.
6. Sa se verifice daca o matrice A(3,3) de tip intreg, este sau nu o matrice simetrica.
7. Se da un vector B de 15 elemente de tip intreg. Sa se creeze matricea triunghiulara A[5][5] cu elementele nenule deasupra diagonalei principale. Sa se adune matricea A cu matricea transpusa a acesteia .
8. Se dă o
matrice de dimensiune 10x10 cu trei elemente nenule. Precizaţi cum va fi
memorată matricea şi calculaţi randamentul obţinut.
9. Scrieti functiile de conversie din matrice simpla in matrice rara si invers.